Работа выполняется по шаблону в среде "Mathcad" (Atulab2.mcd).

Динамические свойства систем автоматического управления и их звеньев могут быть однозначно определены переходной и импульсной (весовой) временными характеристиками. Для получения указанных характеристик на вход системы (звена) подают определенное воздействие u(t) и исследуют реакцию системы (звена) y(t) на это воздействие.

В данной и последующих лабораторных работах свойства звена системы анализируются при помощи входного скачкообразного сигнала (ступенчатое воздействие):

X(t) = 1(t) = 0,   t ≤ 0;    X(t) = 1(t) = 1,  t > 0.

Реакцию анализируемого звена системы на единичное ступенчатое воздействие 1(t) в математической форме описывает переходная функция H(t).

До приложения единичного воздействия звено или система находится в состоянии покоя. Предполагается, что выходная единица имеет ту же размерность, что и физическая переменная на входе системы. В реальных условиях подобное воздействие соответствует быстрому включению задающего сигнала.
 

Апериодическое инерционное звено первого порядка описывается дифференциальным уравнением: T dy/dt + y(t) = k u(t). Передаточная функция звена: W(p) = k/(Tp+1).

Динамические свойства определяются значениями двух величин k и Т. Т – постоянная времени, k – коэффициент передачи (усиления) звена.

Переходная функция: H(p) = W(p) 1(p) = k/[p(Tp+1)].     H(t) = k (1-exp(-t/T)

Весовая функция: h(t) = (k/T) exp(-t/T) 1(t).

АФЧХ инерционного звена: W(jw) = k/(Tjw+1) = k(Tjw-1)/[(Tjw+1)(Tjw-1)] =

k [1/( T²w² +1) - jTw/( T²w² +1)]= k exp(-j arctg Tw) /.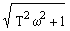

ЛАЧХ и ЛФЧХ инерционного звена: L(w) = 20 lg |W(jw)| = 20 lg k – 10 lg(T²w²+1).

Чем меньше инерционность звена (меньше Т), тем шире полоса пропускания.